개발자로 살아남기

이진 탐색 트리 (Binary Search Tree, BST)

이진 탐색 트리 (Binary Search Tree, BST)

• 이진 트리의 일종
• 데이터를 트리에 저장하는 규칙에 따라야 함
• 노드에 저장된 키 값은 유일해야 함
• 왼쪽 자식 노드 키 > 부모 노드 키 > 오른쪽 노드 키
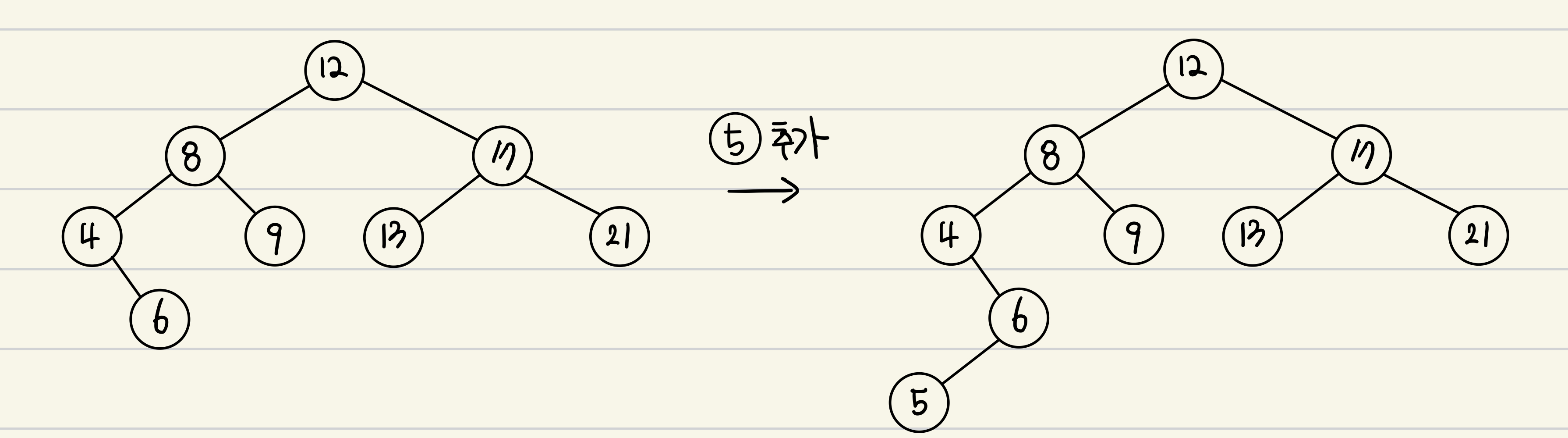
• 삽입할 데이터가 부모 노드보다 작으면 왼쪽, 크면 오른쪽에 삽입
• 왼쪽과 오른쪽의 서브 트리도 이진 탐색 트리
  

  

이진 탐색 트리 구현 방법

• 삽입
  부모 노드와 삽입할 데이터를 비교해서 삽입할 데이터가 더 크면 오른쪽에 추가하고, 더 작으면 왼쪽에 추가한다. 단, 비교할 대상이 없을때까지 내려가야 한다.
  

  

• 탐색
  삽입과 마찬가지로 찾고자하는 데이터가 부모 노드보다 작으면 왼쪽, 크다면 오른쪽으로 탐색한다. 단, 탐색 도중 데이터를 찾았거나 마지막까지 탐색했다면 탐색을 중지한다.
  
  
• 삭제
  임의의 노드(데이터)를 삭제하는 경우 삭제 후에도 이진 탐색 트리가 유지되도록 빈자리를 채워야 한다. 삭제에는 아래 3가지 경우가 있어 각각 다른 방식으로 삭제를 해야한다. 
  1) 단말 노드를 삭제할 경우
  2) 하나의 자식 노드를 가진 노드를 삭제할 경우
  3) 두 개의 자식 노드를 가진 노드를 삭제할 경우
  
  

1) 단말 노드를 삭제할 경우

2) 하나의 자식 노드를 가진 노드를 삭제할 경우

10을 삭제할 경우 자식 노드 13을 10의 위치로 복사하고 13의 노드를 삭제한다.

3) 두 개의 자식 노드를 가진 노드를 삭제할 경우

13을 이동시킨 이유는 이진 탐색 트리는 부모 노드의 왼쪽은 부모 노드보다 작은값, 오른쪽은 큰 값이 되어야 하므로 13을 이동시켰음. 18을 이동시켜도 상관없음

구현

• [BinaryTree.java]
  

  package BinarySearchTree;
  
  public class BinaryTree {
      BTreeNode createBTreeNode() {
          BTreeNode newNode = new BTreeNode();
          newNode.leftNode = null;
          newNode.rightNode = null;
  
          return newNode;
      }
  
      int getData(BTreeNode node) {
          return node.data;
      }
  
      void setData(BTreeNode node, int data) {
          node.data = data;
      }
  
      BTreeNode getLeftSubTree(BTreeNode node) {
          return node.leftNode;
      }
  
      BTreeNode getRightSubTree(BTreeNode node) {
          return node.rightNode;
      }
  
      void createLeftSubTree(BTreeNode parent, BTreeNode child) {
          if (parent.leftNode != null){
              parent.leftNode = null;
          }
  
          parent.leftNode = child;
      }
  
      void createRightSubTree(BTreeNode parent, BTreeNode child) {
          if (parent.rightNode != null) {
              parent.rightNode = null;
          }
  
          parent.rightNode = child;
      }
  
      // 중위 순회
      void InorderTraverse(BTreeNode node) {
          if (node == null){
              return;
          }
  
          InorderTraverse(node.leftNode);
          System.out.println(node.data);
          InorderTraverse(node.rightNode);
      }
  
      // 전위 순회
      void PreorderTraverse(BTreeNode node) {
          if (node == null) {
              return;
          }
  
          System.out.println(node.data);
          PreorderTraverse(node.leftNode);
          PreorderTraverse(node.rightNode);
      }
  
      // 후위 순회
      void PostorderTraverse(BTreeNode node) {
          if (node == null) {
              return;
          }
  
          PostorderTraverse(node.leftNode);
          PostorderTraverse(node.rightNode);
          System.out.println(node.data);
      }
  }​

• [BTreeNode.java]
  

  package BinarySearchTree;
  
  public class BTreeNode {
      int data;
      BTreeNode leftNode;
      BTreeNode rightNode;
  }

• [BST.java]
  

  package BinarySearchTree;
  
  public class BST extends BinaryTree {
      private BTreeNode rootNode = null;
  
      public void insert(int data) {
          // 첫 데이터가 추가됐을 때
          if (rootNode == null) {
              rootNode = new BTreeNode();
              setData(rootNode, data);
              return;
          }
  
          BTreeNode curNode = rootNode;
          BTreeNode parentNode = null;
          // 현재 노드에 데이터가 없을때까지 반복
          while(curNode != null) {
              // 키는 유일해야 하므로 중복값이 있을 경우 빠져나옴
              if (getData(curNode) == data) {
                  return;
              }
  
              // 자식노드가 없을 때 데이터 추가를 위해 부모노드의 값을 유지하고 있어야 함
              parentNode = curNode;
              // 현재 노드의 값이 삽입할 데이터의 값보다 크면 현재 노드의 왼쪽 서브트리에 데이터가 있다는 것이 되므로 왼쪽을 반환
              if (getData(curNode) > data) {
                  curNode = getLeftSubTree(curNode);
              }
              else {
                  curNode = getRightSubTree(curNode);
              }
          }
  
          BTreeNode newNode = new BTreeNode();
          setData(newNode, data);
  
          // 부모 노드의 값이 삽입할 데이터보다 크면 부모 노드의 왼쪽에 데이터를 삽입해야 하므로 왼쪽에 데이터를 등록함
          if (getData(parentNode) > data) {
              createLeftSubTree(parentNode, newNode);
          }
          else {
              createRightSubTree(parentNode, newNode);
          }
      }
  
      // 단순 검색 (존재 유무만 판단함)
      public boolean search(int data) {
          BTreeNode curNode = rootNode;
  
          // 현재 가리키고 있는 노드가 null일 때까지 반복해서 확인
          while(curNode != null) {
  
              // 현재 노드의 값이 찾으려는 대상과 같으면 true
              if (getData(curNode) == data) {
                  return true;
              }
              // 현재 노드의 값이 찾으려는 대상의 값보다 크면 왼쪽 서브트리에 찾을 대상이 있다는 것이므로 현재 노드의 왼쪽을 반환
              else if (getData(curNode) > data){
                  curNode = getLeftSubTree(curNode);
              }
              else {
                  curNode = getRightSubTree(curNode);
              }
          }
  
          return false;
      }
  
      public boolean remove(int data) {
          // 삭제할 노드가 있는지 검색
          BTreeNode deleteNode = rootNode;
          BTreeNode deleteParentNode = null;
          while (deleteNode != null && getData(deleteNode) != data) {
              deleteParentNode = deleteNode;
  
              if (getData(deleteNode) > data) {
                  deleteNode = getLeftSubTree(deleteNode);
              }
              else {
                  deleteNode = getRightSubTree(deleteNode);
              }
          }
  
          // 찾는 데이터가 없다면 false
          if (deleteNode == null) {
              return false;
          }
  
          // 단말노드 삭제 시
          if (getLeftSubTree(deleteNode) == null && getRightSubTree(deleteNode) == null) {
              if (getLeftSubTree(deleteParentNode) == deleteNode) {
                  removeLeftSubTree(deleteParentNode);
              }
              else {
                  removeRightSubTree(deleteParentNode);
              }
          }
          // 자식노드가 하나인 노드 삭제 시
          else if (getLeftSubTree(deleteNode) == null || getRightSubTree(deleteNode) == null) {
              // 삭제할 데이터가 부모노드의 왼쪽에 있는지 오른쪽에 있는지 확인
              if (getLeftSubTree(deleteParentNode) == deleteNode) {
                  // 부모노드의 왼쪽값이 null이 아니면 왼쪽에 데이터가 있다는 것이므로
                  // 부모노드의 왼쪽과 삭제할 데이터의 왼쪽을 연결해 이어줌
                  if (getLeftSubTree(deleteNode) != null) {
                      deleteParentNode.leftNode = deleteNode.leftNode;
                  }
                  // 부모노드의 오른쪽값이 null이 아니면 오른쪽에 데이터가 있다는 것이므로
                  // 부모노드의 왼쪽과 삭제할 데이터의 오른쪽을 연결해 이어줌
                  else {
                      deleteParentNode.leftNode = deleteNode.rightNode;
                  }
              }
              else {
                  if (getRightSubTree(deleteNode) != null) {
                      deleteParentNode.rightNode = deleteNode.rightNode;
                  }
                  else {
                      deleteParentNode.rightNode = deleteNode.leftNode;
                  }
              }
          }
          // 자식노드가 둘인 노드 삭제 시
          else {
              // 이진 탐색 트리의 특성 상 부모의 오른쪽 서브트리에서 가장 작은 값으로 부모노드를 변경해주어야 함
              BTreeNode replaceNode = getRightSubTree(deleteNode);
              BTreeNode replaceParentNode = deleteNode;
              while(getLeftSubTree(replaceNode) != null) {
                  replaceParentNode = replaceNode;
                  replaceNode = getLeftSubTree(replaceNode);
              }
              // 위 로직을 거치면 deleteNode는 삭제할 노드 대신 들어갈 노드를 가리키고,
              // deleteParentNode는 대신 들어갈 노드의 부모를 가리키게 됨.
  
              setData(deleteNode, getData(replaceNode));
  
              // 대신 들어갈 노드의 부모 노드의 왼쪽이 대신 들어갈 노드라면
              // 대신 들어갈 노드의 오른쪽 서브트리를 부모 노드의 왼쪽으로 연결한다.
              if (getLeftSubTree(replaceParentNode) == replaceNode) {
                  replaceParentNode.leftNode = replaceNode.rightNode;
              }
              // 대신 들어갈 노드의 부모 노드의 오른쪽이 대신 들어갈 노드라면
              // 부모 노드의 오른쪽을 대신 들어갈 노드의 오른쪽 노드와 연결한다.
              else {
                  replaceParentNode.rightNode = replaceNode.rightNode;
              }
          }
  
          return true;
      }
  
      private void removeLeftSubTree(BTreeNode node) {
          BTreeNode removeNode = node.leftNode;
          node.leftNode = null;
          removeNode = null;
      }
  
      private void removeRightSubTree(BTreeNode node) {
          BTreeNode removeNode = node.rightNode;
          node.rightNode = null;
          removeNode = null;
      }
  
      // 중위 순회
      void InorderTraverse(BTreeNode node) {
          if (node == null){
              return;
          }
  
          InorderTraverse(node.leftNode);
          System.out.print(node.data + " ");
          InorderTraverse(node.rightNode);
      }
  
      public void showAll() {
          InorderTraverse(rootNode);
          System.out.println();
      }
  }​

• [BSTMain.java]
  

  package BinarySearchTree;
  
  public class BSTMain {
      public static void main(String[] args) {
          BST bst = new BST();
  
          bst.insert(5); bst.insert(8);
          bst.insert(1); bst.insert(6);
          bst.insert(4); bst.insert(9);
          bst.insert(3); bst.insert(2);
          bst.insert(7);
          bst.showAll();
  
          bst.remove(3); bst.showAll();
          bst.remove(8); bst.showAll();
          bst.remove(1); bst.showAll();
          bst.remove(6); bst.showAll();
      }
  }​

• 테스트
  

  

두 개의 자식 노드가 있는 노드를 삭제할 때 헷갈린 부분이 있었다.

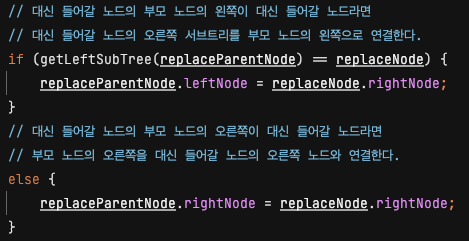
처음에는 대체할 부모의 노드의 왼쪽은 당연히 대체할 노드일 것이라고 생각해서 위 코드가 이해가 되지 않았다. 그러나 아래 그림을 삭제에 대입해서 생각해보니 당연한 얘기였다.

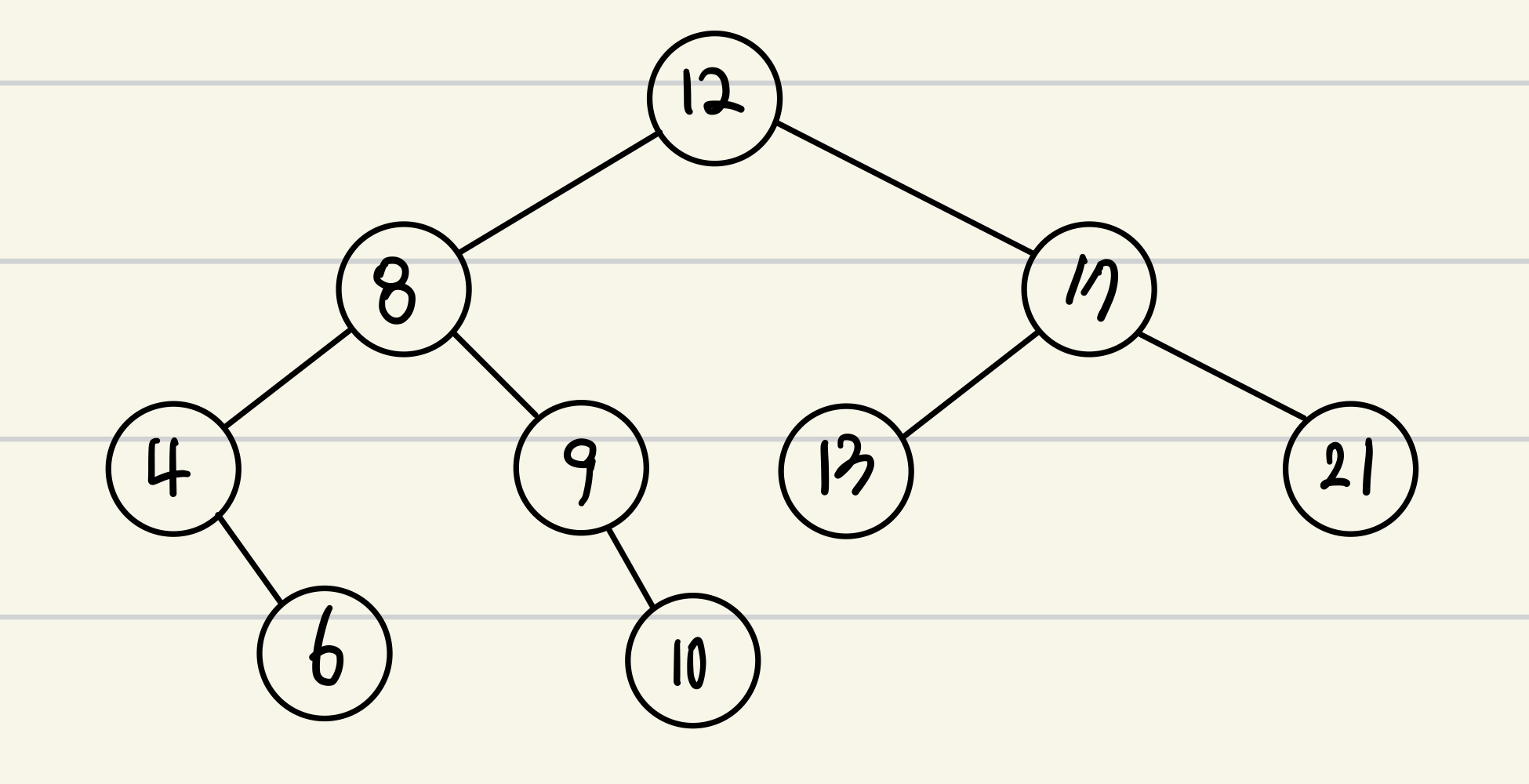
12를 삭제 시 위 코드의 if문에 들어가게 되고, 8을 삭제 시 else 문을 들어가게 된다. 데이터는 12, 8, 4, 6, 9, 10, 17, 13, 21 을 넣고 테스트해보면 된다. 

트리 (Tree)

트리 (Tree)

• 비선형 자료구조
• 계층적 관계를 표현하는 자료구조
  (일상생활에서 사용하는 회사의 조직도 등)
• 여러 노드가 하나의 노드를 가리킬 수 없는 구조 (아래 그림은 트리가 아님)
  

  

용어 정리

• 노드 (node)
   - 트리의 구성요소로, 위 그림에서 A, B, C, D, E, F가 이에 해당됨
• 간선 (edge)
   - 노드와 노드를 연결하는 선
• 루트 노드 (root node)
   - 위 그림의 트리구조에서 최상위에 존재하는 A를 의미
• 단말노드 (terminal node) 또는 잎사귀 노드 (leaf node)
   - 다른 노드가 연결되어있지 않은 노드로서 위 그림에서 E, F, C, D가 이에 해당됨
• 내부노드 (internal node) 또는 비단말 노드 (nonterminal node)
   - 단말노드를 제외한 모든 노드로서, A, B가 이에 해당됨
• 레벨
   - 각 층에 숫자를 매기는 것
  

  

• 높이
   - 트리의 최고레벨을 가리킴
  

  

노드와의 관계

• 노드 A는 B, C, D의 부모 노드이다. (parent)
• B, C, D는 노드 A의 자식 노드이다. (child)
• B, C, D는 부모가 같으므로 형제 노드이다. (sibling)

이진트리 (Binary Tree)와 서브트리 (Sub Tree)

서브트리 (Sub Tree)

• 큰 트리에 속하는 작은 트리
  

  

• 서브트리에 서브트리도 가능

이진트리 (Binary Tree)

• 루트노드로부터 두 개의 서브트리가 존재해야 함
  

  

• 노드가 있어야 할 곳에 노드가 존재하지 않으면 공집합 노드가 존재하는 것으로 간주함
  (노드가 하나여도 두 개의 공노드가 있다고 간주하기 때문에 노드가 하나여도 이진트리가 됨)
  

  

포화 이진트리 (Full Binary Tree)와 완전 이진트리 (Complete Binary Tree)

• 포화 이진트리
   - 모든 레벨에 노드가 가득 찬 상태이며 노드를 더 추가하기 위해서는 레벨을 늘려야 함
  

  

• 완전 이진트리
   - 노드가 트리의 왼쪽부터 순서대로 채워진 것
  

  

• 아래 사진처럼 왼쪽부터 채워지지 않은 경우 이진트리이지만, 완전 이진트리가 아님
  

  

연결리스트 기반 이진트리

• 추상자료형 (ADT)
  

  자료형	반환값	내용
  createBTreeNode()	BTreeNode	이진트리 노드 생성
  getData(BTreeNode)	Data	이진트리 노드의 데이터 반환
  setData(BTreeNode, Data)	void	노드에 데이터 저장
  getLeftSubTree(BTreeNode)	BTreeNode	왼쪽 서브트리를 반환
  getRightSubTree(BTreeNode)	BTreeNode	오른쪽 서브트리를 반환
  createLeftSubTree(BTreeNode, BTreeNode)	void	왼쪽에 서브트리를 연결
  createRightSubStree(BTreeNode, BTreeNode)	void	오른쪽에 서브트리를 연결

  
  
  

연결리스트 기반 이진트리 구현

• 디렉토리 구조
  

  

• BTreeNode.java
  

  package BinaryTree.LinkedList;
  
  public class BTreeNode {
      Object data;
      BTreeNode leftNode;
      BTreeNode rightNode;
  }​

• BinaryTree.java
  

  package BinaryTree.LinkedList;
  
  public class BinaryTree {
      BTreeNode createBTreeNode() {
          BTreeNode newNode = new BTreeNode();
          newNode.leftNode = null;
          newNode.rightNode = null;
  
          return newNode;
      }
  
      Object getData(BTreeNode node) {
          return node.data;
      }
  
      void setData(BTreeNode node, Object data) {
          node.data = data;
      }
  
      BTreeNode getLeftSubTree(BTreeNode node) {
          return node.leftNode;
      }
  
      BTreeNode getRightSubTree(BTreeNode node) {
          return node.rightNode;
      }
  
      void createLeftSubTree(BTreeNode parent, BTreeNode child) {
          if (parent.leftNode != null){
              parent.leftNode = null;
          }
  
          parent.leftNode = child;
      }
  
      void createRightSubTree(BTreeNode parent, BTreeNode child) {
          if (parent.rightNode != null) {
              parent.rightNode = null;
          }
  
          parent.rightNode = child;
      }
  }​

  
  
  
• BinaryTreeMain.java
  

  package BinaryTree.LinkedList;
  
  public class BinaryTreeMain {
      public static void main(String[] args) {
          BinaryTree binaryTree = new BinaryTree();
  
          BTreeNode node1 = binaryTree.createBTreeNode();
          BTreeNode node2 = binaryTree.createBTreeNode();
          BTreeNode node3 = binaryTree.createBTreeNode();
          BTreeNode node4 = binaryTree.createBTreeNode();
          BTreeNode node5 = binaryTree.createBTreeNode();
  
          binaryTree.setData(node1, 'A');
          binaryTree.setData(node2, 'B');
          binaryTree.setData(node3, 'C');
          binaryTree.setData(node4, 'D');
          binaryTree.setData(node5, 'E');
  
          binaryTree.createLeftSubTree(node1, node2); // B를 A의 왼쪽 서브트리로 등록
          binaryTree.createRightSubTree(node1, node3); // C를 A의 오른쪽 서브트리로 등록
          binaryTree.createLeftSubTree(node2, node4); // D를 B의 왼쪽 서브트리로 등록
          binaryTree.createRightSubTree(node2, node5); // E를 B의 오른쪽 서브트리로 등록
  
          BTreeNode tmpNode = null;
          System.out.println(binaryTree.getData(node1)); // 루트 노드 데이터 반환
  
          tmpNode = binaryTree.getLeftSubTree(node1);
          System.out.println(binaryTree.getData(tmpNode)); // A의 왼쪽 서브트리 데이터 반환
  
          tmpNode = binaryTree.getRightSubTree(node1);
          System.out.println(binaryTree.getData(tmpNode)); // A의 오른쪽 서브트리 데이터 반환
  
          tmpNode = binaryTree.getLeftSubTree(node2);
          System.out.println(binaryTree.getData(tmpNode)); // B의 왼쪽 서브트리 데이터 반환
  
          tmpNode = binaryTree.getRightSubTree(node2);
          System.out.println(binaryTree.getData(tmpNode)); // B의 오른쪽 서브트리 데이터 반환
      }
  }​

  
  
  
• 결과
  

  

  

이진트리의 순회

• 전위순회 (Preorder Traversal) : 루트 노드를 먼저 순회
  

  

• 중위순회 (Inorder Traversal) : 루트 노드를 중간에 순회
  

  

• 후위순회 (Postorder Traversal) : 루트 노드를 마지막에 순회
  

  

  
  
  
• 중위순회 방법
   - 재귀적으로 순회 가능
  

  

  1) 왼쪽 서브트리 순회
  2) 루트 노드 방문
  3) 오른쪽 서브트리 순회
  
  
• 중위순회 구현
  

  // 중위 순회
  void InorderTraverse(BTreeNode node) {
      if (node == null){
          return;
      }
  
      InorderTraverse(node.leftNode);
      System.out.println(node.data);
      InorderTraverse(node.rightNode);
  }​

• 전위순회 및 후위순회
   - 중위순회의 방법 1, 2, 3의 순서를 변경
   - 중위순회
  

  // 전위 순회
  void PreorderTraverse(BTreeNode node) {
      if (node == null) {
          return;
      }
  
      System.out.println(node.data);
      PreorderTraverse(node.leftNode);
      PreorderTraverse(node.rightNode);
  }

   - 후위순회
  

  // 후위 순회
  void PostorderTraverse(BTreeNode node) {
      if (node == null) {
          return;
      }
  
      PostorderTraverse(node.leftNode);
      PostorderTraverse(node.rightNode);
      System.out.println(node.data);
  }​

• 순회결과
  

  

  

이진트리를 이용한 수식 표현 (수식트리)

이진트리를 이용한 수식 표현 (수식트리)

• 부모노드의 자식노드 두 개를 피연산자로 한 후 연산
  ex) 7+4*2-1
  

  

이진트리를 이용한 수식 구현

1. 중위표기법을 후위표기법으로 변환
   중위 표기법을 바로 트리로 구현하기 어려움 (괄호 또는 연산자 우선순위 때문에)
   
   
2. 후위표기법을 수식트리로 변환
   스택을 이용하여 구현
   1) 후위표기법의 앞에서부터 스캔
   2) 스캔한 문자가 숫자인 경우 스택에 저장
   3) 스캔한 문자가 연산자인 경우 스택에서 두 개를 꺼내 연결한 후 다시 스택에 저장
   

   public BTreeNode createExpTree(String exp){
       String postfixExp = PostfixNotation.convPostfix(exp);
       Stack<BTreeNode> stack = new Stack<>();
   
       char c = ' ';
       for(int i=0; i<postfixExp.length(); i++){
           node = createBTreeNode();
           c = postfixExp.charAt(i);
   
           // 숫자면
           if (Character.isDigit(c)){
               setData(node, Character.getNumericValue(c));
           }
           // 숫자가 아니면 (연산자면) 연결
           else {
               setData(node, c);
               createRightSubTree(node, stack.pop());
               createLeftSubTree(node, stack.pop());
           }
           stack.push(node);
       }
   
       return stack.pop();
   }​

   
   ex) 중위표기법 1+2+3
   

   후위표기법	스택	결과
   12+3+
   +3+	2  1
   3+
   3+
   +	3

3. 수식트리 계산
    - 재귀로 구현
   1) 단말노드까지 왼쪽으로 이동 (노드의 좌우가 null일 경우) 후 값 반환
   2) 단말노드까지 오른쪽으로 이동 (노드의 좌우가 null일 경우) 후 값 반환
   3) 부모노드 값(연산자) 반환
   4) 연산자에 맞게 계산 진행
   5) 1) ~ 4) 항목 반복
   

   public double calculate(BTreeNode node){
       double op1 = 0;
       double op2 = 0;
   
       // 단말노드인지 확인
       if (getLeftSubTree(node) == null && getRightSubTree(node) == null){
           // 단말노드일 경우 해당 노드의 값을 가져와 Double 형식으로 변환
           return Double.valueOf(getData(node).toString());
       }
   
       // 노드의 왼쪽 피연산자 값 반환
       op1 = calculate(getLeftSubTree(node));
       // 노드의 오른쪽 피연산자 값 반환
       op2 = calculate(getRightSubTree(node));
   
       // 연산자 확인 후 계산
       switch (String.valueOf(getData(node))){
           case "+":
               return op1+op2;
   
           case "-":
               return op1-op2;
   
           case "*":
               return op1*op2;
   
           case "/":
               return op1/op2;
       }
   
       return 0;
   }

구현

• 후위표기법으로 변환을 위한 클래스 생성
  

  package Stack;
  
  import Stack.Stack;
  import Stack.LinkedList.LinkedListStack;
  
  public class PostfixNotation {
      public static String convPostfix(String infix){
          char c = ' ';
          Stack opStack = new LinkedListStack();
          StringBuilder sb = new StringBuilder();
  
          for(int i=0; i<infix.length(); i++){
              c = infix.charAt(i);
  
              // 숫자이면 표현
              if (Character.isDigit(c)){
                  sb.append(c);
              }
              // 연산자 스택이 비어있을 경우 값 push
              else if (opStack.isEmpty()){
                  opStack.push(c);
              }
              // 숫자가 아니고 연산자 스택이 비어있지 않은 경우 (연산자가 하나라도 스택에 추가된 경우)
              else {
                  // 여는 괄호가 나오면 스택에 저장 후 다음 문자로
                  if (c == '('){
                      opStack.push(c);
                      continue;
                  }
                  // 닫는 괄호가 나올 경우
                  // 스택에 저장된 모든 연산자를 반환
                  else if (c == ')'){
                      char check = ' ';
                      while(true) {
                          check = (char) opStack.pop();
                          if (check == '(') {
                              break;
                          }
                          else {
                              sb.append(check);
                          }
                      }
                      continue;
                  }
  
                  // 현재 연산자의 우선순위가 더 높은 경우
                  // 스택에 연산자 저장
                  if (compareOp((char)opStack.peek(), c) > 0){
                      opStack.push(c);
                  }
                  // 현재 연산자의 우선순위가 더 낮거나 같은 경우
                  // 스택에 있는 우선순위가 높은 연산자를 빼서 표현
                  else {
                      while(!opStack.isEmpty()){
                          if (compareOp((char)opStack.peek(), c) <= 0){
                              sb.append(opStack.pop());
                          }
                          else {
                              break;
                          }
                      }
                      opStack.push(c);
                  }
              }
          }
  
          char check = ' ';
          while(!opStack.isEmpty()) {
              check = (char) opStack.pop();
              if (check != '(') {
                  sb.append(check);
              }
          }
  
          return sb.toString();
      }
  
      // 연산자 우선순위 반환
      public static int getOpPriority(char c){
          switch (c) {
              case '*':
              case '/':
                  return 3;
  
              case '+':
              case '-':
                  return 2;
  
              case '(':
                  return 1;
  
              default:
                  return -1;
          }
      }
  
      // 연산자 우선순위 비교
      public static int compareOp(char stackOp, char curOp){
          int stackOpPriority = getOpPriority(stackOp);
          int curOpPriority = getOpPriority(curOp);
  
          // 현재 우선순위가 더 높은 경우
          if (stackOpPriority < curOpPriority){
              return 1;
          }
          // 우선순위가 같은 경우
          else if (stackOpPriority == curOpPriority){
              return 0;
          }
          // 스택의 우선순위가 더 높은 경우
          else {
              return -1;
          }
      }
  }​

• 수식트리 구현을 위한 클래스 (BinaryTree 상속)
  

  package BinaryTree.LinkedList;
  
  import java.util.Stack;
  import Stack.PostfixNotation;
  
  public class ExpressionTree extends BinaryTree {
      BTreeNode node;
  
      public BTreeNode createExpTree(String exp){
          String postfixExp = PostfixNotation.convPostfix(exp);
          Stack<BTreeNode> stack = new Stack<>();
  
          char c = ' ';
          for(int i=0; i<postfixExp.length(); i++){
              node = createBTreeNode();
              c = postfixExp.charAt(i);
  
              // 숫자면
              if (Character.isDigit(c)){
                  setData(node, Character.getNumericValue(c));
              }
              // 숫자가 아니면 (연산자면) 연결
              else {
                  setData(node, c);
                  createRightSubTree(node, stack.pop());
                  createLeftSubTree(node, stack.pop());
              }
              stack.push(node);
          }
  
          return stack.pop();
      }
  
      public double calculate(BTreeNode node){
          double op1 = 0;
          double op2 = 0;
  
          // 단말노드인지 확인
          if (getLeftSubTree(node) == null && getRightSubTree(node) == null){
              // 단말노드일 경우 해당 노드의 값을 가져와 Double 형식으로 변환
              return Double.valueOf(getData(node).toString());
          }
  
          // 노드의 왼쪽 피연산자 값 반환
          op1 = calculate(getLeftSubTree(node));
          // 노드의 오른쪽 피연산자 값 반환
          op2 = calculate(getRightSubTree(node));
  
          // 연산자 확인 후 계산
          switch (String.valueOf(getData(node))){
              case "+":
                  return op1+op2;
  
              case "-":
                  return op1-op2;
  
              case "*":
                  return op1*op2;
  
              case "/":
                  return op1/op2;
          }
  
          return 0;
      }
  }​

  
  
  
• 수식트리 테스트 구현
  

  package BinaryTree.LinkedList;
  
  public class ExpressionTreeMain {
      public static void main(String[] args) {
          ExpressionTree expTree = new ExpressionTree();
  
          BTreeNode expNode = expTree.createExpTree("(1+2)*3");
          System.out.println(expTree.calculate(expNode));
      }
  }​

  
  
  
• 결과
  

  

[참고] 열혈 자료구조

[전체코드] 

스택 (Stack)

스택 (Stack)

• 선형 자료구조
• 프링글스처럼 한 쪽은 막혀있고 다른 한 쪽으로 과자를 꺼내거나 넣는 것
• 후입선출 (Last-In, First-Out, LIFO) 구조
  마지막에 삽입한 것이 먼저 나오는 구조
• 배열 또는 리스트로 구현 가능

추상 자료형 (ADT)

배열로 스택 구현

• 배열의 크기를 고정해야 함
• 스택에서 가장 마지막에 삽입된 위치를 저장하는 변수가 필요 (topIndex)

구현

• 디렉토리 구조
  

  

• ArrayStack.java
  

  package Stack.Array;
  
  import Stack.Stack;
  
  public class ArrayStack implements Stack {
      // 스택 배열의 최대 크기
      final private int MAX_SIZE = 10;
      // 가장 마지막에 삽입된 데이터의 위치
      int topIndex = -1;
      // 스택 설정
      Object[] stack = new Object[MAX_SIZE];
  
      @Override
      public void initialize() {
          // 배열을 null로 초기화
          for(int i=0; i<MAX_SIZE; i++) {
              stack[i] = null;
          }
          // -1 => 아무것도 삽입되지 않음
          topIndex = -1;
      }
  
      @Override
      public void push(Object data) {
          if (topIndex == MAX_SIZE - 1){
              System.out.println("더이상 공간이 없습니다.");
              return;
          }
  
          // 데이터 삽입
          stack[++topIndex] = data;
      }
  
      @Override
      public Object pop() {
          if (isEmpty()){
              System.out.println("데이터가 없습니다.");
              return null;
          }
  
          // 데이터 반환 후 삭제
          return stack[topIndex--];
      }
  
      @Override
      public Object peek() {
          if (isEmpty()){
              System.out.println("데이터가 없습니다.");
              return null;
          }
  
          return stack[topIndex];
      }
  
      @Override
      public boolean isEmpty() {
          if (topIndex == -1){
              return true;
          }
  
          return false;
      }
  }​

• ArrayStackMain.java
  

  package Stack.Array;
  import Stack.Stack;
  
  public class ArrayStackMain {
      public static void main(String[] args) {
          Stack stack = new ArrayStack();
          stack.initialize();
  
          stack.push(1); stack.push(2);
          stack.push(3); stack.push(4);
          stack.push(5); stack.push(6);
  
          while(!stack.isEmpty()){
              System.out.println(stack.pop());
          }
      }
  }​

리스트로 스택 구현

• 머리에 데이터를 삽입하는 연결 리스트와 동일
  

  

구현

• 디렉토리 구조
  

  

• LinkedListStack.java
  

  package Stack.LinkedList;
  import Stack.Stack;
  
  public class LinkedListStack implements Stack {
  
      public class Node {
          Object data;
          Node nextNode;
      }
  
      Node head = null;
  
      @Override
      public void initialize() {
          head = null;
      }
  
      @Override
      public void push(Object data) {
          Node newNode = new Node();
          newNode.data = data;
          newNode.nextNode = head;
          head = newNode;
      }
  
      @Override
      public Object pop() {
          if (isEmpty()){
              System.out.println("데이터가 없습니다.");
              return null;
          }
  
          Object rData = head.data;
          head = head.nextNode;
  
          return rData;
      }
  
      @Override
      public Object peek() {
          if (isEmpty()) {
              System.out.println("데이터가 없습니다.");
              return null;
          }
  
          return head.data;
      }
  
      @Override
      public boolean isEmpty() {
          if (head == null){
              return true;
          }
  
          return false;
      }
  }​

• LinkedListStackMain.java
  

  package Stack.LinkedList;
  
  import Stack.Array.ArrayStack;
  import Stack.Stack;
  
  public class LinkedListStackMain {
      public static void main(String[] args) {
          Stack stack = new LinkedListStack();
          stack.initialize();
  
          stack.push(1); stack.push(2);
          stack.push(3); stack.push(4);
          stack.push(5); stack.push(6);
  
          while(!stack.isEmpty()){
              System.out.println(stack.pop());
          }
      }
  }​

시간복잡도란?

(Time Complexity)

시간복잡도라는 말 자체가 뭔가 되게 모순되어 보인다.. 그래도 한 번 살펴보자.

시간복잡도 (Time Complexity)

 - 입력 데이터가 특정 알고리즘을 거쳐 결과가 나오는데 걸리는 시간을 의미

   여기서 "시간"은 정확히 몇 초 걸린다! 그런 의미가 아닌 데이터의 증가에 따른 시간(연산속도)의 증가 정도를 의미

 - 시간복잡도는 대입연산, 사칙연산, 비교구문, 함수호출 등의 연산을 기준으로 계산

 - 시간복잡도는 최선, 평균, 최악의 경우로 나눌 수 있음

빅-오(Big-O) 표기법

 - 단순히 시간복잡도를 표현한 다항식에서 최고차항의 차수가 빅-오가 된다.

 - 예를들어, 100n^3 + 99999n^2 + 888 이라는 시간복잡도를 가진 함수가 있을 때, 이 다항식을 빅-오 표기법으로 표현하면 O(n^3)이 된다. 99999n^2도 상당히 큰 수인데 제외하는 이유는 단순히 시간복잡도는 위에 언급한 것처럼 데이터의 증가에 따른 시간(연산횟수)의 증가 정도를 표현하기 때문이다. 

빅-오(Big-O) 표기법에 따른 계산방법

 - 다음과 같은 코드가 있을 때의 시간복잡도를 빅-오로 표현하면 어떻게 될까?

for(int i=0; i<sizeof(arr)/sizeof(int); i++){
	if (arr[i] == 7){
    	printf("7 => index %d\n", i + 1);
        break;
    }
}

배열 arr의 크기를 모르며 어떤 데이터가 들어있는지 모른다는 최악의 상황을 가정하고 구해보면 다음과 같다.

연산을 기준으로 시간복잡도를 구한다고 했으니

이 된다. 따라서 위 코드의 시간복잡도는 T(n) = 3n + 1이 되며, 이를 빅-오로 표현하면 최고차항의 차수인 O(n)이 된다.

마지막으로 아래 사진은 대표적인 빅-오 이다.

자료구조와 각 정렬 방법의 빅-오는 아래 사이트를 참고하면 된다.

https://www.bigocheatsheet.com/

자료구조란 무엇인가?

자료구조가 무엇인지 위키백과를 확인해보면 자료구조는 효율적인 접근 및 수정을 가능하게 하는 자료의 조직, 관리, 저장을 의미한다고 나와있다. 즉, 당연한 말이지만 위의 말 그대로 자료를 어떻게 구성(조직)할 것이고 어떤 방식으로 관리하고 저장할 것인지를 말한다.

자료구조는 알고리즘과 밀접한 관계를 맺고 있는데, 한가지 간단한 예를 들어보면 다음과 같다.

위 예시에서 홈런볼은 "자료"를 의미한다. 그리고 이 홈런볼들을 모아놓은 박스를 "조직"이라고 할 수 있다. 즉, 관련있는 것들(홈런볼)을 어떤 방식으로 구성(박스)할 것인지를 말한다. 그리고 유통기한 순서대로 홈런볼을 판매하는데 이것을 "관리"라고 할 수 있다. 이 박스들을 유통기한 순서대로 가장 길게 남은 박스는 아래에 두고 위로는 유통기한이 짧은 박스를 쌓아두는데 이 쌓아두는 것을 "저장"이라고 할 수 있다. 마지막으로 맨 위에 쌓여있는 박스를 바닥으로 내려 홈런볼을 꺼내는 행위를 "알고리즘"이라고 할 수 있다.

나중에 배우게 될 자료구조이지만 위 저장방식은 LIFO(Last-In First-Out)로 나중에 들어간 데이터가 먼저 나오는 자료구조인 스택을 이용하였으며, 알고리즘은 이 자료구조를 이용하여 어떻게 문제를 해결하는지를 말한다. 즉, 자료구조가 결졍되어야 그에 맞는 알고리즘을 결정할 수 있기 때문에 자료구조와 알고리즘은 밀접한 관계를 맺고 있다고 볼 수 있다. 물론 자료구조가 달라지면 알고리즘도 바뀌어야 한다. 위 예시에서 스택 자료구조가 아닌 큐(Queue) 자료구조가 쓰인다면 그에 맞는 알고리즘(맨 위의 상자를 아래로 내린 후 홈런볼을 꺼내는 행위)도 바뀌어야 한다는 뜻이다.